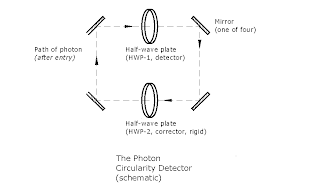
Proposal summary: can we find circularity of a single photon along a range of values?

Suppose a photon is a superposition of e.g. 0.8|RH> and 0.6 |LH>. Standard QM says we can only test for the 64%/36% chance of getting full "RH" or "LH" as projected eigenstates. But let's use mirrors to send a single photon round and round many times through a pair of half-wave plates ("pair", to revert the photon to original state for entry.) HWPs flip the rotation of polarized light. They accumulate angular momentum thereby (Beth experiment 1936 etc.) That AM is proportional to the circularity of the light times the number of photons. Hence it shows intermediate values for elliptical light etc.

From particle indistinguishability: the same photon going through each HWP many times (being reverted to original state each pass through two HWPs) should have the effect of the same number of like photons, going through once each. Hence, I argue, we should get a range of results for circularity (intermediate for elliptical, no net AM change for linear, etc.) for one photon as for many. But that contradicts standard theory, so what happens?