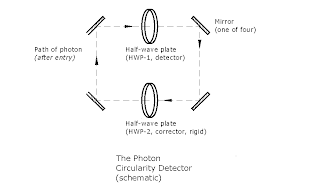
Proposal summary: can we find circularity of a single photon along a range of values?
Suppose a photon is a superposition of e.g. 0.8|RH> and 0.6 |LH>. Standard QM says we can only test for the 64%/36% chance of getting full "RH" or "LH" as projected eigenstates. But let's use mirrors to send a single photon round and round many times through a pair of half-wave plates ("pair", to revert the photon to original state for entry.) HWPs flip the rotation of polarized light. They accumulate angular momentum thereby (Beth experiment 1936 etc.) That AM is proportional to the circularity of the light times the number of photons. Hence it shows intermediate values for elliptical light etc.
From particle indistinguishability: the same photon going through each HWP many times (being reverted to original state each pass through two HWPs) should have the effect of the same number of like photons, going through once each. Hence, I argue, we should get a range of results for circularity (intermediate for elliptical, no net AM change for linear, etc.) for one photon as for many. But that contradicts standard theory, so what happens?
From particle indistinguishability: the same photon going through each HWP many times (being reverted to original state each pass through two HWPs) should have the effect of the same number of like photons, going through once each. Hence, I argue, we should get a range of results for circularity (intermediate for elliptical, no net AM change for linear, etc.) for one photon as for many. But that contradicts standard theory, so what happens?
Labels: quantum measurement paradox
posted by Neil Bates at 19:45
8 Comments:
This comment has been removed by the author.
Hi Neil,
It’s nice to see that you are still persuing your attempt to expose the standard treatment of QM as being inadequate. The fact is however that ever since J.S. Bell’s inequality was confirmed it’s been clear that the interpretation of QM being insufficient to explain it’s formalism, as although it requires the results found it lends no explanation as to account for them other than to say that QM is not a classical theory, which is simply another way to say it doesn’t provide one. Like I said before the consequence of this being is that most who take QM seriously now understand this and rather to assign things as never to be understood most now are dependent on believing a explanations for reality which borders on having it rather be no more then a dream.
This I would say is a sad state of affairs for a discipline that is supposed to have reality present as being more reasonably rational rather than less. Also, I as you applaud Penrose for his efforts and in part agree with his objections and conclusions, all but one, and that in not to extend his thinking that gravity may represent as being a consequence of one aspect of nature being holistic, while particle behaviour being another. As you seem to have his book Roads to Reality and have read his arguments I’m somewhat surprised that you didn’t notice his case against the Bohmian model being entirely philosophical and nothing more. After discovering this I found it strange that for someone who has caught the scent as their being something rotten in Copenhagen (rather than Denmark), that he’s still unprepared to go the further step to realize that any explanation founded on a singular ontological explanations (as aspects of substance) just won’t cut it.
“It has been often said, and certainly not without justification, that the man of science is a poor philosopher. Why, then, should it not be the right thing for the physicist to let the philosopher to the philosophizing? Such might indeed be the right thing at a time when the physicist believes he has at his disposal a rigid system of fundamental concepts and fundamental laws which are also well established that waves of doubt cannot reach them; but, it cannot be right at a time when the very foundations of physics itself become problematic as they are now. At a time like the present, when experience forces us to seek a newer and more solid foundation, the physicist cannot simply surrender to the philosopher the critical contemplation of the theoretical foundations; for, he himself knows best, and feels more surely where the shoe pinches. In looking for a new foundation he must make clear in his own mind just how far such concepts which he uses are justified, and are necessities.”
-Albert Einstein “Physics and Reality” for the journal of the Franklin Institute [Volume.221, No. 3, March 3, 1936]
I find it strange that on one hand that those in the discipline can applaud the accomplishments of their most brilliant peers, yet continue to be so deaf when it comes to their pleas for reason which form to be at the very heart as to how tjey were done.
Best,
Phil
Hi Neil,
Predictably, I'll argue that the single-photon and many-photon cases are not equivalent, and that the standard theory's prediction for the single photon case should be borne out.
One issue--which just goes towards refuting overall equivalence--is that a single photon can't dump unlimited amounts of angular momentum on the HWPs. Otherwise they'd acquire unlimited rotational kinetic energy and you'd have a perpetual motion machine! Energy is conserved via the (experimentally demonstrated) rotational Doppler effect; as the HWPs spin up, the photon's frequency decreases towards zero. Eventually it gets to some sort of ground state where its kinetic energy is less than the transition energy between rotation states of the HWPs. After that, I would guess, the photon will zip right through the HWPs without flipping state.
Since the frequency changes on each pass, the photon isn't reverting to its original state, and it's not really equivalent to sending many photons with the original frequency through once each. In the latter case, the HWPs would just keep spinning up to some ridiculous rotation speed (unless the beam was pure linear, anyway).
Before I get into the other argument--and yes, I'm probably going to argue for entanglement again--do you propose to perform one strong measurement on the HWPs after many passes have elapsed, to determine their net angular momentum change? Or are we continuously performing weak measurements (or strong ones, as you prefer) on them as the passes occur? I'm all for the former option, since I find it simpler to think about, but you're making the rules!
Anton, you have a point about the energy transfer. The HWP would pick up kinetic energy K during n passes of the photon such that K = Iω²/2 and angular momentum buildup (from rest) to S = Iω = 2nħ. Juggling around we find
K = 2n²ħ²/I.
Well, ħ is tiny and ħ² even more so, but I need to look at the quantitative and will get back to you. Note that it would be odd for physical issues like moment of inertia to be just the amount to get in the way of a measurement principle. Note also, although it might have to be the same in principle, that we can use torsion etc. and not let the disk actually rotate up to speed (?) Also, we can "in principle" have a more complicated, sufficiently achromatic HWP which could start with a high enough energy photon of superposed circularity C such that 2nCħ = 2nħ(a²— b²) is detectable before that happens.
As for the QM, I can't blame you for conventional expectations, but this situation is paradoxical. In order to avoid the consequence of intermediate spin detection, you'd have to keep in effect two sets of books for the photon. You need to violate the principle that the WF already encodes what effect it will have on objects. Note that in real entanglement, the correlations *are encoded* in the combined wave functions. But the exit photon switches RH and LH coefficients, and frequency is not relevant to the associated angular momentum. Maybe there is "more" but if there is, that is new physics and I "win" anyway IMHO.
I say "it's worth looking into" however the analysis turns out.
BTW, years ago I thought of an energy paradox along just the lines of the rotational Doppler shift, but for any single pass of a fully CP photon, parallel spins. Consider that the transferred angular momentum is 2ħ and (if this time, the disk is already rotating) the extra kinetic energy transfer is dK = ωdS = 2ħω. Well, suppose the energy of the photon is indeed less than 2ħω, then what? You could say it's "forbidden" but what happens to the photon?
You can make it less embroiled in polarization etc. by considering simple absorption into a spinning disk. Like, a long IR photon into a disk spinning really fast. The problem is similar. I wonder what happens? Must it be scattered off? And even then, there is change of angular momentum which has to go somewhere.
Just to cover all the "side issues" with rotational Doppler effects in one go....
Note also, although it might have to be the same in principle, that we can use torsion etc. and not let the disk actually rotate up to speed (?)
You can, although then the disk will act as an oscillator, and you'll have the same effect (I think) with the photon gradually bumping it up to higher energy levels, until the photon's frequency is too low to pack enough energy to make it to the next level.
And if you simply damp the disk's motion, you couple the system to the external environment, and (from a decoherence perspective) basically collapse the photon's wavefunction on every pass...
Also, we can "in principle" have a more complicated, sufficiently achromatic HWP which could start with a high enough energy photon of superposed circularity C such that 2nCħ = 2nħ(a²— b²) is detectable before that happens.
An achromatic HWP would be a good trick, since they generally only work for one specific wavelength! But sure, I don't think there's anything wrong with pretending one exists here.
Consider that the transferred angular momentum is 2ħ and (if this time, the disk is already rotating) the extra kinetic energy transfer is dK = ωdS = 2ħω. Well, suppose the energy of the photon is indeed less than 2ħω, then what? You could say it's "forbidden" but what happens to the photon?
My wild guess would be that it simply passes through the disk (or maybe reflects)--if it's forbidden from interacting, it won't interact. (This wouldn't be terribly surprising; isn't long-wave radio relatively immune to absorption for precisely this reason?
Like, a long IR photon into a disk spinning really fast. The problem is similar. I wonder what happens? Must it be scattered off? And even then, there is change of angular momentum which has to go somewhere.
True. But if the photon's simply reflected back the way it came, it can preserve angular momentum by switching helicities. And if the photon's scattered off-axis, that angular momentum could go into changing the disk's axis of rotation, or adding a wobble. That might not require a prohibitive amount of energy.
Or, again, it may just ghost through the disk. Perhaps an ideal disk which can absorb photons of any wavelength is just too far from reality to be a useful intuition pump here!
Back to the main event!
In order to avoid the consequence of intermediate spin detection, you'd have to keep in effect two sets of books for the photon.
Isn't the wave function keeping two sets of books for you? The system starts out as, say, (a|LH> + b| RH>) ⊗ |0> ⊗ |0> --that is, a separable product of three states: the photon polarization state, the rotational state of the first HWP and the rotational state of the second HWP. (The HWP states are here labeled with their associated angular momenta, which start at zero.)
When the photon hits the first HWP, you get entanglement, and the system becomes (b|LH> ⊗ |+2ħ> + a|RH> ⊗ |-2ħ>) ⊗ |0>. Entanglement is encoded in the fact that the system state is no longer a single vector product of HWP and photon states. When the photon hits the second HWP, all three "objects" become entangled, and you get (a|LH> ⊗ |-2ħ> ⊗ |+2ħ> + b|RH> ⊗ |+2ħ> ⊗ |-2ħ>). The two product states in the sum are orthogonal, so thereafter they propagate independently, with each state's first factor flipping between |LH> and |RH> and the HWP factors alternately incrementing by ±2ħ --those are your two sets of books.
After n passes through both HWPs, the system state is a( |LH> ⊗ |-2nħ> ⊗ |+2nħ>) + b( |RH> ⊗ |-2nħ> ⊗ |+2nħ>). If a precise angular momentum measurement is then made on either HWP, the system collapses into one of the two product states--no intermediate values allowed.
In the multiphoton case, on the other hand, it's not that the system doesn't keep two sets of books, but rather that it keeps n+1 sets of books, each corresponding to a different distribution of photon helicities. It can do this because lots of photons = lots of degrees of freedom. (As you say, one photon is indistinguishable from another--but that doesn't mean one photon is indistinguishable from an ensemble of multiple photons!) You still have entanglement until measurement occurs, and measurement still collapses your wave function from a superposition of product states down to a single product state. But now there are n+1 product states to collapse into, not just two. And most of those product states correspond to intermediate angular momentum values, in which some of the photons are right-handed and some are left-handed.
But the exit photon switches RH and LH coefficients, and frequency is not relevant to the associated angular momentum.
Switching coefficients doesn't break the correlation, though; every time they switch, one of the HWPs increments its momentum to match. Whenever you decide to make the measurements on the HWPs, it will still be possible to infer the photon's helicity with certainty.
I say "it's worth looking into" however the analysis turns out.
Oh, without doubt. It's a very enlightening scenario.
Anton, first of all: thank you very much for being so interested in this and other of my "paradoxes." Could you do me a favor? Try to get people interested in them, especially this one. Aside from whether I'm right about what happens (and I'm not sure, it's just suggestive), I am sure this is an interesting thought experiment to explore the neglected (?) area of repeated interactions by a single particle.
Note I do not mean the type of "weak measurement" recently in the news, about plotting average paths of many photons in a double slit experiment. I am trying to find a sort of "average" of a single photon. Even if the outcome is just a chance of getting full LH or RH spin, we'll need new ways to represent things like the pre-measurement detector carrying multiples of the interaction state (like spin) compared to the particle. More on the details later, but the bottom line is: this concept matters. Yes the experiment would be hard to do, but theorists should be looking into it
Post a Comment
<< Home