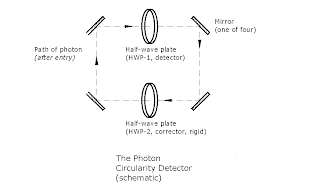
Proposal summary: can we find circularity of a single photon along a range of values?
From particle indistinguishability: the same photon going through each HWP many times (being reverted to original state each pass through two HWPs) should have the effect of the same number of like photons, going through once each. Hence, I argue, we should get a range of results for circularity (intermediate for elliptical, no net AM change for linear, etc.) for one photon as for many. But that contradicts standard theory, so what happens?
Labels: quantum measurement paradox